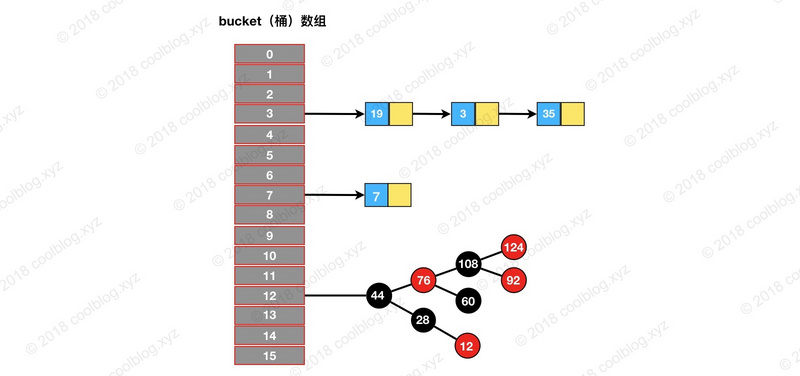
HashMap 数据结构图:

HashMap 的数据结构是由数组和链表+红黑树组成。在进行增删查等才做的时候的时候会先定义到桶的位置,然后遍历桶的链表找到该元素。例如查询元素35,步骤如下:
- 定位到元素
35所在的桶的位置:index = 35 % 16 = 3
- 在遍历
3号桶找到该元素
由于 HashMap 的数组大小会动态改变,因此元素的桶的值可能会因为桶数组的改变而改变。
在JDK 1.8 中,HashMap 引入了红黑树,即 HashMap 的底层数据结构由原来的数组+链表变为数组+链表+红黑树。
# HashMap 源码分析
查找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
if (first.hash == hash &&
((k = first.key) == key || (key != null && key.equals(k))))
return first;
if ((e = first.next) != null) {
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
|
我们先来看看查找过程的第一步 - 确定桶位置,其实现代码如下:
1
| first = tab[(n - 1) & hash]
|
由于桶的大小总是2的幂,所以此时,(n - 1) & hash 其实是等效于对 length 取余,只不过使用位运算的效率高于取余操作。
插入
插入的流程有些类似与查询,因此很容易想到大致流程。首先肯定是先定位要插入的键值对属于哪个桶,定位到桶后,再判断桶是否为空。如果为空,则将键值对存入即可。如果不为空,则需将键值对接在链表最后一个位置,或者更新键值对。看起来很简单,但实际上还要考虑扩容的问题。并且在 JDK 1.8 中 HashMap 还引入了红黑树,因此还要考虑当链表过长的时候使用红黑树进行优化。
首先看一下插入的源码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1)
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) {
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
|
扩容机制
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
| final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1;
} else if (oldThr > 0)
newCap = oldThr;
else {
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else {
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
|
上面的源码有点长,希望大家耐心看懂它的逻辑。上面的源码总共做了3件事,分别是:
- 计算新桶数组的容量 newCap 和新阈值 newThr
- 根据计算出的 newCap 创建新的桶数组,桶数组 table 也是在这里进行初始化的
- 将键值对节点重新映射到新的桶数组里。如果节点是 TreeNode 类型,则需要拆分红黑树。如果是普通节点,则节点按原顺序进行分组。
# 笔记
为什么 HashMap 的容量为 2 的幂次?
HashMap 的默认容量是 16,而当我们去指定一个容量,例如Map map = new HashMap(25) 的时候,HashMap 会调用一个 tableSizeFor(val) 方法,将传进去的容量变为大于等于该值的 2 的幂次,也就是说我传进一个 25,而 HashMap 的初始容量却为 32。也就是说无论我们指定的初始值为多少,初始容量一定为 2 的幂次
那么为什么 HashMap 的容量一定要为 2 的幂次呢?
在 putVal 方法中,有这样一段代码
1
| first = tab[(n - 1) & hash]
|
其中,tab 指的是 HashMap 中的数组,var8 指的是数组长度,hash 指的是传进来的 key 的 hash 值。
(n - 1) & hash 这段翻译过来就是 length - 1 & hash(key),也就是取 key 的 hash 对数组长度减一取模。
为什么说是取模呢,举个例子,当我们的 length 等于 16 时:
16 的二进制: 0001 0000
16-1的二进制: 0000 1111
这个时候这个操作等价与于 hash(key) % (lenth-1),而位与操作的效率显然比直接 % 取模的操作的效率高得多。
假设我们的 length 不是2的幂次,假设它是 17,此时:
17-1的二进制: 0001 0000
这个时候对其进行 & 操作,只会有 0000 0000 和 0001 0000 两种可能,这样会增加我们哈希碰撞的概率,使得查询的效率大大下降。
PS:经实验,位与 & 运算的效率是 取模 % 运算的十倍不止。
为什么 HashMap 的最大容量为 2 的 30 次幂?
众所周知,Java中 int 的最大值是 2^31-1,而 HashMap 中的容量为 2 的幂次,所以是 2 的30次幂
为什么 HashMap 是线程不安全的?
为什么默认负载因子是 0.75?
若负载因子过高,当数据量较多时,更容易产生 hash 碰撞,导致查询效率降低;
若负载因子过低,则会导致 HashMap 的空间利用率低;
牛顿二项式
为什么链表转红黑树默认阈值是 8?
正常来说链表长度的概率符合泊松分布:
$$
(λt)^ne^{-λt}\over n!
$$
在负载因子为0.75的情况下,链表长度的概率为:
1
2
3
4
5
6
7
8
9
| >0: 0.60653066
>1: 0.30326533
>2: 0.07581633
>3: 0.01263606
>4: 0.00157952
>5: 0.00015795
>6: 0.00001316
>7: 0.00000094
>8: 0.00000006
|
当长度为8的时候,概率是非常小的,此时进行树化是比较合适的时机
虽然阈值为8,但是当树化的时候,链表实际长度为9
树化除了要达到阈值,Map中的数组长度必须还要大于等于 64;当达到阈值但数组长度小于64时,会进行扩容